再谈协方差矩阵之主成分分析

自从上次谈了协方差矩阵之后，感觉写这种科普性文章还不错，那我就再谈一把协方差矩阵吧。上次那篇文章在理论层次介绍了下协方差矩阵，没准很多人觉得这东西用处不大，其实协方差矩阵在好多学科里都有很重要的作用，比如多维的正态分布，再比如今天我们今天的主角——主成分分析(Principal Component Analysis，简称 PCA)。结合 PCA 相信能对协方差矩阵有个更深入的认识~

PCA 的缘起

PCA 大概是 198x 年提出来的吧，简单的说，它是一种通用的降维工具。在我们处理高维数据的时候，为了能降低后续计算的复杂度，在“预处理”阶段通常要先对原始数据进行降维，而 PCA 就是干这个事的。本质上讲，PCA 就是将高维的数据通过线性变换投影到低维空间上去，但这个投影可不是随便投投，要遵循一个指导思想，那就是：找出最能够代表原始数据的投影方法。这里怎么理解这个思想呢？“最能代表原始数据”希望降维后的数据不能失真，也就是说，被 PCA 降掉的那些维度只能是那些噪声或是冗余的数据。这里的噪声和冗余我认为可以这样认识：

噪声：我们常说“噪音污染”，意思就是“噪声”干扰我们想听到的真正声音。同样，假设样本中某个主要的维度 A，它能代表原始数据，是“我们真正想听到的东西”，它本身含有的“能量”(即该维度的方差，为啥？别急，后文该解释的时候就有啦~)本来应该是很大的，但由于它与其他维度有那么一些千丝万缕的相关性，受到这些个相关维度的干扰，它的能量被削弱了，我们就希望通过 PCA 处理后，使维度 A 与其他维度的相关性尽可能减弱，进而恢复维度 A 应有的能量，让我们“听的更清楚”！
冗余：冗余也就是多余的意思，就是有它没它都一样，放着就是占地方。同样，假如样本中有些个维度，在所有的样本上变化不明显(极端情况：在所有的样本中该维度都等于同一个数)，也就是说该维度上的方差接近于零，那么显然它对区分不同的样本丝毫起不到任何作用，这个维度即是冗余的，有它没它一个样，所以 PCA 应该去掉这些维度。

这么一分析，那么 PCA 的最终目的就是“降噪”和消灭这些“冗余”的维度，以使降低维度的同时保存数据原有的特征不失真。后面我们将结合例子继续讨论。

协方差矩阵——PCA 实现的关键

前面我们说了，PCA 的目的就是“降噪”和“去冗余”。“降噪”的目的就是使保留下来的维度间的相关性尽可能小，而“去冗余”的目的就是使保留下来的维度含有的“能量”即方差尽可能大。那首先的首先，我们得需要知道各维度间的相关性以及个维度上的方差啊！那有什么数据结构能同时表现不同维度间的相关性以及各个维度上的方差呢？自然是非协方差矩阵莫属。回忆下浅谈协方差矩阵的内容，协方差矩阵度量的是维度与维度之间的关系，而非样本与样本之间。协方差矩阵的主对角线上的元素是各个维度上的方差(即能量)，其他元素是两两维度间的协方差(即相关性)。我们要的东西协方差矩阵都有了，先来看“降噪”，让保留下的不同维度间的相关性尽可能小，也就是说让协方差矩阵中非对角线元素都基本为零。达到这个目的的方式自然不用说，线代中讲的很明确——矩阵对角化。而对角化后得到的矩阵，其对角线上是协方差矩阵的特征值，它还有两个身份：首先，它还是各个维度上的新方差；其次，它是各个维度本身应该拥有的能量(能量的概念伴随特征值而来)。这也就是我们为何在前面称“方差”为“能量”的原因。也许第二点可能存在疑问，但我们应该注意到这个事实，通过对角化后，剩余维度间的相关性已经减到最弱，已经不会再受“噪声”的影响了，故此时拥有的能量应该比先前大了。看完了“降噪”，我们的“去冗余”还没完呢。对角化后的协方差矩阵，对角线上较小的新方差对应的就是那些该去掉的维度。所以我们只取那些含有较大能量(特征值)的维度，其余的就舍掉即可。PCA 的本质其实就是对角化协方差矩阵。

下面就让我们跟着上面的感觉来推推公式吧。假设我们有一个样本集 X，里面有 N 个样本，每个样本的维度为 d。即：

$X=\\{X\_1,\ldots,X\_N\\} \quad X\_i=(x\_{i1},\ldots,x\_{id})\in\mathcal{R}^d, i=1,\ldots,N$

将这些样本组织成样本矩阵的形式，即每行为一个样本，每一列为一个维度，得到样本矩阵 S：$S\in\mathcal{R}^{N\times d}$。我们先将样本进行中心化，即保证每个维度的均值为零，只需让矩阵的每一列除以减去对应的均值即可。很多算法都会先将样本中心化，以保证所有维度上的偏移都是以零为基点的。然后，对样本矩阵计算其协方差矩阵，按照《浅谈协方差矩阵》里末尾的 update，我们知道，协方差矩阵可以简单的按下式计算得到：

$C=\frac{S^T S}{N-1} \quad C\in\mathcal{R}^{d\times d}$

下面，根据我们上文的推理，将协方差矩阵 C 对角化。注意到，这里的矩阵 C 是是对称矩阵，对称矩阵对角化就是找到一个正交矩阵 P，满足：$P^TCP=\Lambda$。具体操作是：先对 C 进行特征值分解，得到特征值矩阵(对角阵)即为$\Lambda$，得到特征向量矩阵并正交化即为$P$。显然，$P,\Lambda\in\mathcal{R}^{d\times d}$。假如我们取最大的前 p(p<d)个特征值对应的维度，那么这个 p 个特征值组成了新的对角阵$\Lambda_1\in\mathcal{R}^{p\times p}$，对应的 p 个特征向量组成了新的特征向量矩阵$P_1\in\mathcal{R}^{d\times p}$。

实际上，这个新的特征向量矩阵$P_1$就是投影矩阵，为什么这么说呢？假设 PCA 降维后的样本矩阵为$S_1$，显然，根据 PCA 的目的，$S_1$中的各个维度间的协方差基本为零，也就是说，$S_1$的协方差矩阵应该为$\Lambda_1$。即满足：

$\frac{S_1^TS_1}{N-1}=\Lambda_1$

而我们又有公式：

$P^TCP=\Lambda \Rightarrow P_1^TCP_1=\Lambda_1$

代入可得：

$\frac{S_1^TS_1}{N-1}=\Lambda_1=P_1^TCP_1=P_1^T\left(\frac{S^TS}{N-1}\right)P_1=\frac{(SP_1)^T(SP_1)}{N-1}$ $\Rightarrow S_1=SP_1 \quad S_1\in\mathcal{R}^{N\times p}$

由于样本矩阵$S_{N\times d}$的每一行是一个样本，特征向量矩阵$P_{1(d\times p)}$的每一列是一个特征向量。右乘$P_1$相当于每个样本以$P_1$的特征向量为基进行线性变换，得到的新样本矩阵$S_1\in\mathcal{R}^{N\times p}$中每个样本的维数变为了 p，完成了降维操作。实际上，$P_1$中的特征向量就是低维空间新的坐标系，称之为“主成分”。这就是“主成分分析”的名称由来。同时，$S_1$的协方差矩阵$\Lambda_1$为近对角阵，说明不同维度间已经基本独立，噪声和冗余的数据已经不见了。至此，整个 PCA 的过程已经结束，小小总结一下：

形成样本矩阵，样本中心化

2) 计算样本矩阵的协方差矩阵

对协方差矩阵进行特征值分解，选取最大的 p 个特征值对应的特征向量组成投影矩阵

4) 对原始样本矩阵进行投影，得到降维后的新样本矩阵

Matlab 中 PCA 实战

首先，随机产生一个10*3维的整数矩阵作为样本集，10 为样本的个数，3 为样本的维数。

1	S = fix(rand(10,3)*50);

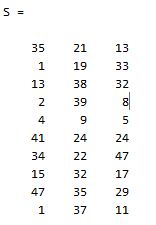
计算协方差矩阵：

S = S - repmat(mean(S),10,1);
C = (S'*S)./(size(S,1)-1);
or
C = cov(S);

对协方差矩阵进行特征值分解：

1	[P,Lambda] = eig(C);

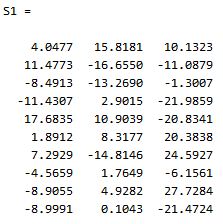
这里由于三个方差没有明显特别小的，所以我们都保留下来，虽然维度没有降，但观察 Lambda(即 PCA 后的样本协方差矩阵)和 C(即原始的协方差矩阵)，可以发现，~~3 个维度上的方差都有增大，也就是能量都比原来增大了，~~3 个维度上的方差有所变化，但对角线之和没有变，能量重新得到了分配，这就是“降噪”的功劳。最后我们得到降维后的样本矩阵：

S1 = S*P;

为了验证，我们调用 matlab 自带的主成分分析函数princomp：

1	[COEFF,SCORE] = princomp(S) % COEFF表示投影矩阵，SCORE表示投影后新样本矩阵

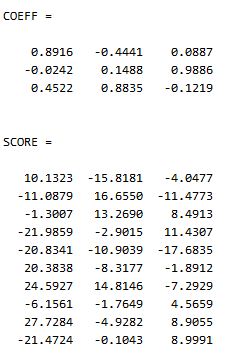
对比，可以发现，SCORE 和$S_1$在不考虑维度顺序和正负的情况下是完全吻合的，之所以我们计算的$S_1$的维度顺序不同，是因为通常都是将投影矩阵 P 按能量(特征值)的降序排列的，而刚才我们用 eig 函数得到的结果是升序。另外，在通常的应用中，我们一般是不使用 matlab 的princomp函数的，因为它不能真正的降维(不提供相关参数，还是我没发现？)。一般情况下，我们都是按照协方差矩阵分解后特征值所包含的能量来算的，比如取 90%的能量，那就从最大的特征值开始加，一直到部分和占特征值总和的 90%为止，此时部分和含有的特征值个数即为 p。

经过了一番推公式加敲代码的过程，相信大家对主成分分析应该不陌生了吧，同时对协方差矩阵也有了更深层次的认识了吧，它可不只是花花枪啊。我个人觉得 PCA 在数学上的理论还是很完备的，想必这也是它能在多种应用中博得鳌头的原因吧。