求解 SDP 问题—使用 SeDuMi 和 YALMIP

SDP(SemiDefinite Programing，半定规划)是凸优化(Convex Optimization)的一种，貌似近些年来比较热，反正这个东西常常出现在我看的论文中。论文里一般是把一个问题转化为 SDP，然后极不负责任的扔了一句可以使用 SeDuMi 等工具箱解决就完事了，搞的本人非常迷茫，于是决定一探究竟，谁知还搞了个意外收获，那就是 YALMIP 工具箱。SeDuMi和YALMIP都是 Matlab 的工具箱，下载和安装请参见它们的主页。下面我就分别谈谈怎么样将两个工具箱应用于 SDP 求解吧。

SDP 问题的对偶原型及求解步骤

下面就是一个典型的 SDP 问题：

$$min \quad c^{T}y \\\\ s.t.\\\\ A\_{1}y = b\_{1} \\\\ A\_{2}y \ge b\_{2} \\\\ F\_{0}+y\_{1}F\_{1}+\ldots+y\_{p}F\_{p} \ge 0$$

目标函数是线性的，有一个等式约束，有一个不等式约束，最后一个是 LMI(Linear Matrix Inequality，线性矩阵不等式)约束。使用 SeDuMi 来解决此类问题，我们就要自行构造调用 SeDuMi 的核心函数sedumi(Att,bt,ct,K)的四个参数。

$$At(:,i) = -vec(F\_{i}) \quad for \quad i = 1,\ldots, p$$ $$Att = \[A\_{1};-A\_{2};At\]$$ $$bt = -c$$ $$ct = \[b\_{1};-b\_{2};vec(F\_{0})\]$$

等式约束的个数: $K.f = size(A_{1},1)$

不等式约束的个数: $K.l = size(A_{2},1)$

LMI 中矩阵的阶数: $K.s = size(F_{0},1)$

这样，我们就可以调用$[x,y,info] = sedumi(Att,bt,ct,K)$来求解了，其中的 y 即为优化后得到的最优解。

一个典型的例子

这里举一个简单的例子，并给出 Matlab 的实际代码，以便能更好地理解运用上节的知识。SDP 的一个最简单的应用就是最大化矩阵的特征值问题。如我们要找$y_{1},y_{2},y_{3}$使矩阵$F = F_{0}+y_{1}F_{1}+y_{2}F_{2}+y_{3}F_{3}$的特征值最大化，其中$F_{0},F_{1},F_{2},F_{3}$分别为：

$$F\_{0} = \begin{bmatrix} 2 & -0.5 & -0.6 \\\\ -0.5 & 2 & 0.4 \\\\ -0.6 & 0.4 & 3 \\\\ \end{bmatrix}, F\_{1} = \begin{bmatrix} 0 & 1 & 0 \\\\ 1 & 0 & 0 \\\\ 0 & 0 & 0 \\\\ \end{bmatrix}, \\\\ \\\\ F\_{2} = \begin{bmatrix} 0 & 0 & 1 \\\\ 0 & 0 & 0 \\\\ 1 & 0 & 0 \\\\ \end{bmatrix}, F\_{3} = \begin{bmatrix} 0 & 0 & 0 \\\\ 0 & 0 & 1 \\\\ 0 & 1 & 0 \\\\ \end{bmatrix}$$

同时，我们对$y_{1},y_{2},y_{3}$也给出一个不等式限制和一个等式限制：

$$0.7 \le y\_{1} \le 1,0 \le y\_{2} \le 0.3,y\_{3} \ge 0$$ $$y\_{1}+y\_{2}+y\_{3} = 1$$

那么这个问题可以描述成以下形式：

$$min \quad t \\\\ s.t.\\\\ A\_{1}y = b\_{1}\\\\ A\_{2}y \ge b\_{2} \\\\ tI-(F\_{0}+y\_{1}F\_{1}+y\_{2}F\_{2}+y\_{3}F\_{3}) \ge 0$$

其中$y,A_{1},A_{2},b_{1},b_{2}$的取值分别为：

$$b\_{1} = 1,b\_{2} = \[0.7,-1,0,-0.3,0\]^T A\_{2} = \begin{bmatrix} 1 & 0 & 0 & 0 \\\\ -1 & 0 & 0 & 0 \\\\ 0 & 1 & 0 & 0 \\\\ 0 & -1 & 0 & 0 \\\\ 0 & 0 & 1 & 0 \\\\ \end{bmatrix}$$

下面我们就可以使用 sedumi 函数进行优化求解了，给出 Matlab 代码：

A1 = [1 1 1 0];
A2 = [1 0 0 0; -1 0 0 0; 0 1 0 0; 0 -1 0 0; 0 0 1 0];
b1 = 1;
b2 = [0.7 -1 0 -0.3 0]';
F0 = [2 -0.5 -0.6; -0.5 2 0.4; -0.6 0.4 3];
F1 = [0 1 0; 1 0 0; 0 0 0];
F2 = [0 0 1; 0 0 0; 1 0 0];
F3 = [0 0 0; 0 0 1; 0 1 0];
F4 = eye(3);
At = -[vec(F1) vec(F2) vec(F3) vec(F4)];
Att = [A1; -A2; At];
bt = -[0 0 0 1]';
ct = [b1; -b2; vec(F0)];
K.f = size(A1,1);
K.l = size(A2,1);
K.s = size(F0,1);
[x,y,info] = sedumi(Att,bt,ct,K);
y

最后得到的 y 即为最优解，它的前三个分量就是我们想要的答案。如下图所示：

YALMIP 一出，谁与争锋

我们从上面也可以看到，SeDuMi 的求解过程还是比较复杂的，不仅需要将优化问题先化成 SDP 的标准形式，而且参数的配置也相当费功夫，很不直观！在搜索 SeDuMi 的过程中，我又发现了一个叫 YALMIP 的工具箱，它的命名挺有意思，Yet Another LMI Package，又一个 LMI 包，呵呵，不过它可不是徒有虚名啊！简单的说，它可以非常直观的将目标函数和约束条件赋给它的核心函数 solvesdp(Constraint,Objective)，下面我们就看看解决同样的问题 YALMIP 是怎么操作的，废话不说了，直接上 Matlab 代码：

t = sdpvar(1); % sdpvar声明变量
y = sdpvar(3,1,'full');
F0 = [2 -0.5 -0.6; -0.5 2 0.4; -0.6 0.4 3];
F1 = [0 1 0; 1 0 0; 0 0 0];
F2 = [0 0 1; 0 0 0; 1 0 0];
F3 = [0 0 0; 0 0 1; 0 1 0];
a = [sum(y)==1]; % 等式约束
b = [0.7<=y(1)<=1, 0<=y(2)<=0.3, y(3)>=0]; %不等式约束
c = [t*eye(3)-(F0 + y(1)*F1 + y(2)*F2 + y(3)*F3)>=0]; % LMI约束
obj = t;
constraint = [a,b,c];
solvesdp(constraint,obj);
double(y)

结果如下图所示：

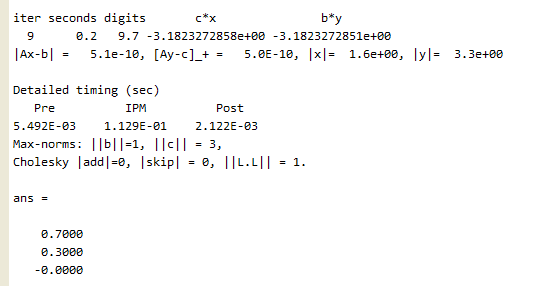
可以看到两者的结果基本是一致的，当然，我怀疑 YALMIP 在操作的过程中有调用 SeDuMi 的可能性，但是不管怎么说，YALMIP 的代码则更直观，更容易理解，甚至连双向不等式都可以直接书写，这都是明显的，可见它的牛逼，所以必然果断抛弃其他一切优化工具箱，你的意见呢？嘿嘿～

P.S. 最近总是学术文章，我也有点受不鸟了～写这玩意累啊，歇着去了。。。